用信息论解决猜词问题

问题的引入

和朋友讨论猜词游戏wordle时突然有人说:

很显然的是，如果考虑到一些密码学知识这个问题会变得非常的复杂，尽管对wordle这种情况其实可以对整个词库进行分析，但是这样这个问题就不是很数学了，所以我们得抽象一下。

问题的描述

Wordle是一个有趣的猜字游戏，这个游戏会提供一个5个字母的词，玩家每次提交一个答案，系统会为这个答案的5个字母分别上色。绿色代表这个字母内容和位置都正确，黄色代表内容正确但位置错了，灰色代表这个字母不在答案中。

现在让我们忽略语言学和密码学知识，假设所有的字母均等概率的出现在每一位，且可以重复。那么对于这样一个随机的单词，我们最少需要猜多少次才能保证一定能猜到正确的单词？

问题的推理

初看这个问题并不是很直观，但是一个贪心的策略是可以简单被构造出来的。

首先，我们需要确定5个字母分别是什么。考虑最坏情况，这些字母至少有一个属于uvwxyz，那么我们可以以以下一个显然的策略来保证一定能在5次之内得到：

ABCDE

FGHIJ

KLMNO

PQRST

UVWXY

这样的话，根据抽屉原理，只要这里黄色的字母有5个，就可以认定一定是这5个字母的排列，而如果不足5个则可以用Z填上。那这里我们不妨假设字母全是黄色的最坏情况，在这种情况下，我们依次先将每个字母摆在他们表现成黄色位置，如果有两个字母在同一列则将其中更靠上的那一个放在左边，如果有Z的话就默认Z在没有字母出现过的位置。不妨假设这组字母就是AGMSY。

现在我们将他们向左循环移一位，得到一个新的词

GMSYA

以此类推，那么在最坏情况下会有

(AGSMY)

GMSYA

MSYAG

SYAGM

这五次所有的字母都是黄色的，那么这样我们就知道答案是

YAGMS

但是发现了一个很显然的错误，尽管如果有重复，我们在位移的过程中也能确认他们的位置，但是这代表在最开始的5次中我们并不知道是否有Z！

也就是说，如果黄色的字母只有4个，我们是没法判断是因为引入了Z还是因为有字母重复出现了2遍的。

所以为了得到一个理论上的下界，让我们请出信息论工具。

首先，很显然的总的信息量是 $H=5\log26$ ，而对猜一次的信息熵，让我们构造一个概率（中间的碰壁过程就略去了，明明只是一个超几何分布，有点傻）

考虑每一位，有三种情况即绿色、黄色和灰色。其中绿色和灰色的概率都很好算，分别是猜中的 $P_{c(orrect)}=\frac1{26}$ 和在5个字母里都没出现的 $P_{w(rong)}=(\frac{25}{26})^5$ ，由此可以间接的方便的得到黄色的概率，即 $P_{p(artial)}=1-P_c-P_w\approx0.14$ 。

在此基础上，我们可以构造一个类似超几何分部的结构，考虑一个单词中有i个字母是绿色，j个字母是灰色，于是有

P_{i,j} = C_5^iP_c^iC_5^jP_w^jC_5^{5-i-j}P_p^{5-i-j}

那么由信息量公式 $H=\sum^n_i{-P_i\log P_i}$ ，我们把所有的式子写在一起

H_{single}=\sum_{i=0}^5\sum_{j=0}^{5-i}-P_{i,j}\log P_{i,j},where

P_{i,j} = C_5^iP_1C_5^jP_2C_5^{5-i-j}P_3,where

P_c=\frac{1}{26}, P_w=(\frac{25}{26})^5, P_p=1-P_c-P_w\approx0.14

写一个简单的python程序计算一下结果(这里的 $P_{i,j}$ 的计算稍微有一些问题，实际以上述公式为准)

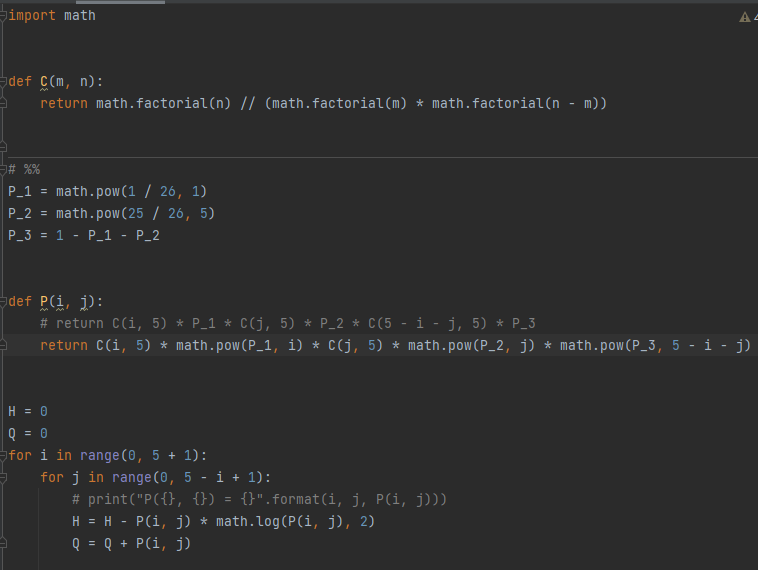
得到 $H_{single}\approx2.28848789899762$ 。在代码中我们进行了一些验算，将所有的 $P_{i,j}$ 加载一起，其和为1的话这个分布的设计就应该没有太大的问题。

最后将两者做除法即可以得到总次数是 $\frac{H}{H_{single}}\approx10.26975<11$

策略的提出

有了这个知识以后我们再来考虑构造策略。

因为足足有11次可用，我们可以构造一个暴力到让这个题目变得非常平凡的策略。

仍然保证1-5不变，通过这样我们可以确认5个可能的字母(包括Z)，让我们假设前面黄色的字母还是AGSM。

但是现在我们很暴力的使用我们剩下的次数。

(AGSM)

AAAAA

GGGGG

SSSSS

MMMMM

ZZZZZ

这样在这5次中我们总可以至少确定一个字母的位置，或者是否有重复，或者是否甚至有重复的Z。

虽然还是和算出来的有一些差异，但是以我不完全的信息论知识来讲，可能与我们提到的26个字母里排除25个就隐含着有z有关，因为我们所建立的概率模型内并没有表现出这一点——我们假设每次试验之间是独立的。因此基于已有的方案给出的结论会带来额外的信息量，如果在我们的方案里模拟该结果的话，无论最后五个可能的字母是什么，都需要在现在的5和6之间插入一条ZZZZZ的猜测。